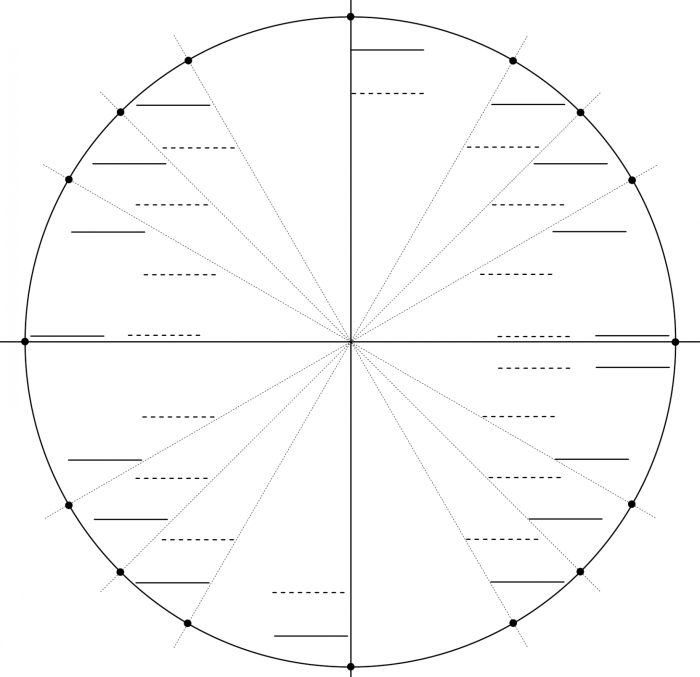
Embark on a journey into the fascinating realm of unit circle fill in the blank answers, where the intricacies of trigonometry unfold. This guide provides a comprehensive exploration of the unit circle, empowering you with the knowledge and techniques to conquer any trigonometry challenge.
Delve into the depths of unit circle definitions and concepts, unraveling the equation that governs its existence and its profound connection to trigonometry. Discover the coordinates of points that reside on the unit circle, mastering the art of finding coordinates and angles with ease.
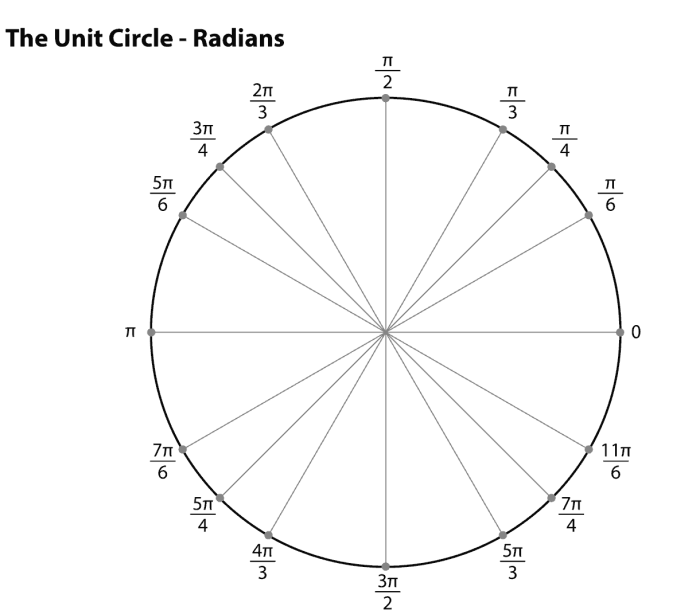
Unit Circle Definitions and Concepts
The unit circle is a circle with radius 1, centered at the origin of the coordinate plane. It is often used to define and visualize trigonometric functions.
The equation of the unit circle is x2+ y 2= 1 . This equation states that the sum of the squares of the x-coordinate and the y-coordinate of any point on the unit circle is equal to 1.
The unit circle is closely related to trigonometry. The sine of an angle is the y-coordinate of the point on the unit circle that corresponds to that angle. The cosine of an angle is the x-coordinate of the point on the unit circle that corresponds to that angle.
Unit Circle Coordinates and Points
The coordinates of the points on the unit circle can be found using the following formulas:
- (cos θ, sin θ)
- (x, y) = (cos θ, sin θ)
For example, the point (1, 0)is on the unit circle at an angle of 0. The point (0, 1)is on the unit circle at an angle of π/2.
To find the angle of a point on the unit circle given its coordinates, we can use the following formulas:
- θ = arctan(y/x)
- θ = arctan(sin θ/cos θ)
For example, the angle of the point (1, 1)is π/4.
Unit Circle Special Angles
The special angles on the unit circle are 0, π/2, π, and 3π/2. These angles have special relationships with the trigonometric functions.
| Angle | Coordinates | Sine | Cosine |
|---|---|---|---|
| 0 | (1, 0) | 0 | 1 |
| π/2 | (0, 1) | 1 | 0 |
| π | (-1, 0) | 0 | -1 |
| 3π/2 | (0,
|
-1 | 0 |
The patterns and relationships between the special angles and their trigonometric values can be used to solve a variety of trigonometry problems.
Unit Circle Applications, Unit circle fill in the blank answers
The unit circle has a variety of applications in trigonometry. It can be used to:
- Find trigonometric values
- Solve trigonometric equations
- Prove trigonometric identities
- Graph trigonometric functions
For example, the unit circle can be used to find the sine of 30 degrees. The point on the unit circle that corresponds to 30 degrees is (√3/2, 1/2). Therefore, the sine of 30 degrees is 1/2.
Frequently Asked Questions: Unit Circle Fill In The Blank Answers
What is the equation of the unit circle?
x^2 + y^2 = 1
How do I find the coordinates of a point on the unit circle given an angle?
x = cos(angle), y = sin(angle)
What are the special angles on the unit circle?
0, π/2, π, 3π/2