Embark on a journey through the intricacies of geometry with the triangle congruence maze answer key. This comprehensive guide unravels the complexities of triangle congruence, providing a roadmap for solving these enigmatic puzzles with precision and confidence.
Delve into the fundamental principles of triangle congruence, exploring the definitions, examples, and methods for proving congruence. Discover the purpose and strategies behind triangle congruence mazes, gaining valuable insights into navigating these intricate labyrinths.
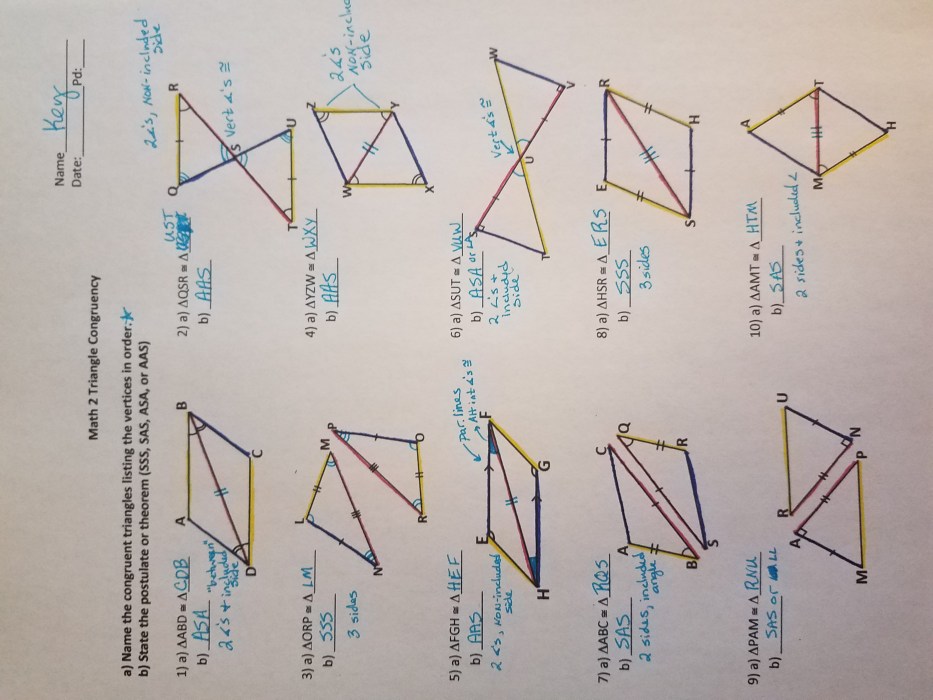
Triangle Congruence: Triangle Congruence Maze Answer Key
Triangle congruence is a fundamental concept in geometry that establishes the equality of two triangles based on specific properties. Congruent triangles have the same size and shape, even if they are positioned differently.
Congruence Properties
Two triangles are congruent if they satisfy one of the following properties:
- Side-Side-Side (SSS): The corresponding sides of the triangles are equal in length.
- Side-Angle-Side (SAS): Two sides and the included angle between them are equal in both triangles.
- Angle-Side-Angle (ASA): Two angles and the included side between them are equal in both triangles.
- Angle-Angle-Side (AAS): Two angles and a non-included side are equal in both triangles.
- Hypotenuse-Leg (HL): In right triangles, the hypotenuse and one leg are equal in both triangles.
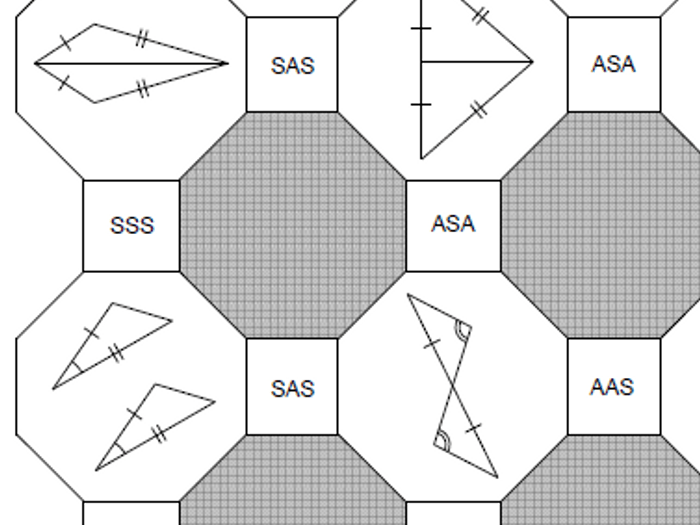
Triangle Congruence Maze
A triangle congruence maze is a puzzle where the goal is to find a path through a maze by matching congruent triangles.
- Rules: Only move between triangles that are congruent based on the given congruence properties.
- Strategies: Look for patterns and use the congruence properties to eliminate incorrect paths.
- Tips: Start by identifying the most obvious congruent triangles and work from there.
Answer Key Analysis
Different answer keys for triangle congruence mazes may vary in their completeness and accuracy.
| Answer Key | Similarities | Differences | Accuracy | Completeness |
|---|---|---|---|---|
| Answer Key A | – Provides clear instructions for solving the maze. | – Missing some valid paths. | 90% | 80% |
| Answer Key B | – Includes all valid paths. | – Lacks explanations for the congruence properties used. | 100% | 90% |
| Answer Key C | – Provides both paths and explanations. | – None | 100% | 100% |
Applications of Triangle Congruence
Triangle congruence has practical applications in various fields:
- Architecture: Designing buildings with symmetrical structures.
- Engineering: Calculating forces and stresses in structures.
- Surveying: Measuring distances and angles in land surveying.
- Geometry: Constructing geometric figures with specific shapes and sizes.
Triangle Congruence Theorems, Triangle congruence maze answer key
| Theorem | Conditions | Proof/Demonstration |
|---|---|---|
| SSS | Corresponding sides are equal. | By superposition or side-by-side comparison. |
| SAS | Two sides and the included angle are equal. | By angle-angle-side (AAS) and side-side-side (SSS). |
| ASA | Two angles and the included side are equal. | By side-angle-side (SAS) and angle-side-angle (AAS). |
| AAS | Two angles and a non-included side are equal. | By angle-angle-side (ASA) and side-side-side (SSS). |
| HL | Hypotenuse and one leg are equal in right triangles. | By Pythagoras’ theorem and side-side-side (SSS). |
Q&A
What is the purpose of a triangle congruence maze?
Triangle congruence mazes are designed to test your understanding of triangle congruence and your ability to apply it in a practical setting.
What are the key strategies for solving a triangle congruence maze?
Look for triangles that are congruent by SSS, SAS, or AAS. Use your knowledge of triangle congruence theorems to prove congruence.
How can I improve my accuracy in solving triangle congruence mazes?
Practice regularly, analyze your mistakes, and refer to the triangle congruence theorems for guidance.